기간 수익률 비교하기
- 데이터프레임의 기준 첫날을 0으로 맞추고 상승했는지 하락했는지 구하기
- 다른 스케일 값의 상승/하락 비교
- 다른 스케일의 값을 조정할 때 표준화 혹은 정규화 방법 사용
- 표준화(standardization) :
- 데이터가 평균으로 부터 얼마나 떨어져 있는지 나타내는 값으로 변환
- (Z-score 표준화) : (측정값 - 평균) / 표준편차
- 표준편차 공식이랑 같음~!!
- 정규화(normalization) :
- 데이터의 상대적 크기에 대한 영향을 줄이기 위해 0~1로 변환
- (측정값 - 최소값) / (최대값 - 최소값)
전체 데이터프레임 값에 대한 수익률 계산하기
- 첫번째 날 가격으로 나머지 가격을 나눠주고 -1을 해주면 수익률을 구할 수 있음
df_norm = (df / df.iloc1[0]) -1 # 수익률 (산 날을 기준으로 나누고 -1 하면 수익률)
df_norm
lg엔솔은 상장하지 기준이 되는 날 상장하지 않았어서 NaN값이 나옴
-> 그래서 상장 전을 dropna 하고 상장날을 기준으로 수익률을 구함
df_norm['LG에너지솔루션'] = (df['LG에너지솔루션']/df['LG에너지솔루션'].dropna().iloc[0]) - 1
df_norm
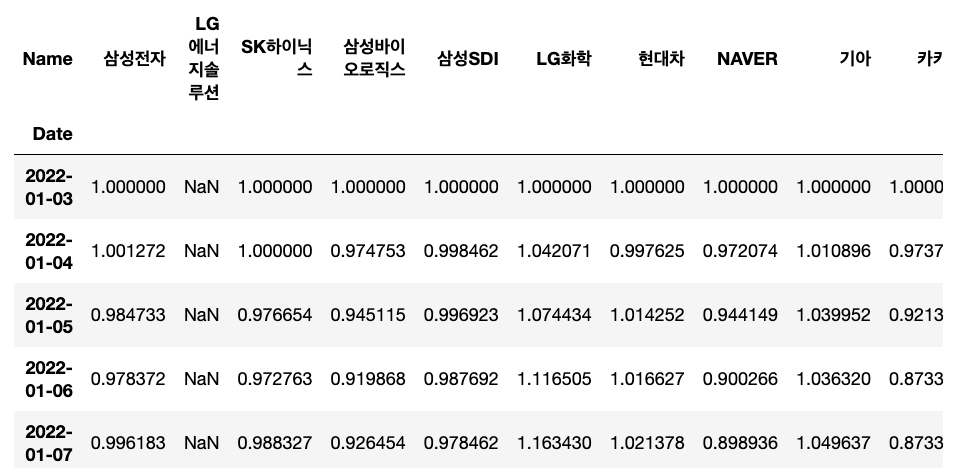
왜 -1 을 해주는 건가 생각해 봤는데
1만원짜리 9천원에 팔면 1천원(=10프로) 할인, 9천원(= 90프로) => 10프로 할인한다고, 정가대비 10프로 싼거니까 같은 의미
전체 종목의 수익률 시각화
# Pandas API -> 조금더 편함
# df_norm 변수에 담긴 전체 종목에 대한 수익률을 시각화
df_norm.plot(figsize = (12, 4))
plt.legend(bbox_to_anchor = (1, 1))
plt.axhline(0, c="k", lw = 0.5)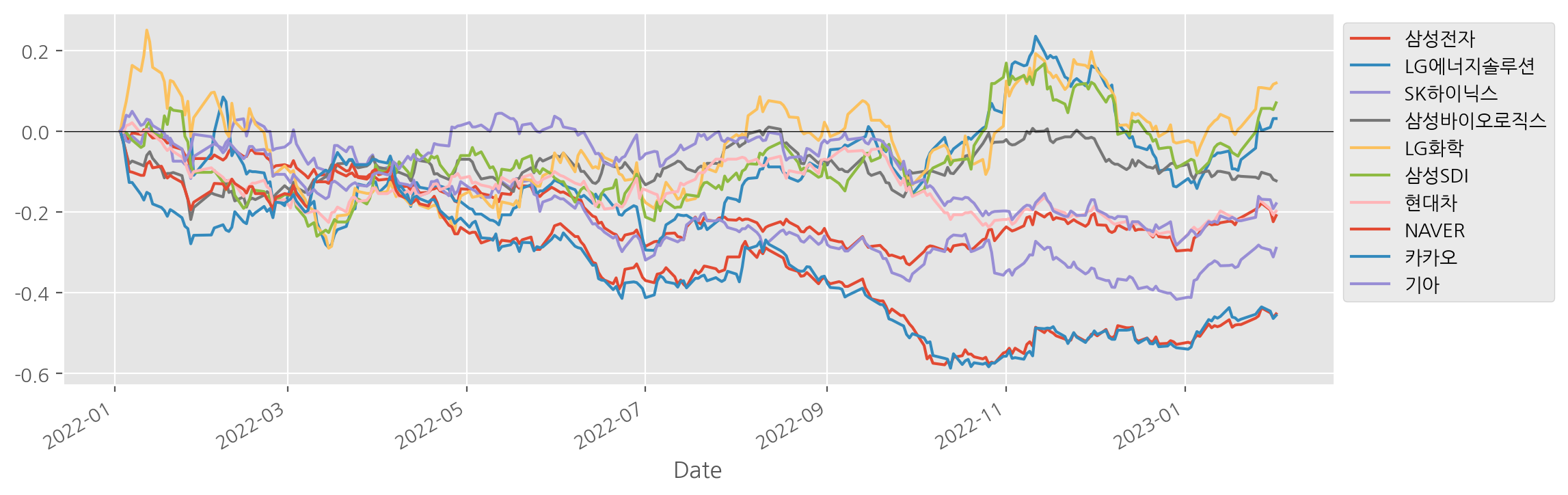
# matplotlib API-> 손이 많이 가는 그래프
plt.plot(df_norm)
plt.axhline(0, c="k", lw = 0.5)
plt.show
matplotlib으로도 그래프 만들 수 있음 but 너무 불편, 복잡 -> 하나하나 다 지정해줘야 함 -> 그래서 판다스 애용
# 시가총액 상위 3개 종목만 시각화
df_norm.iloc[:, :3].plot(figsize = (12, 3))
plt.legend(bbox_to_anchor = (1, 1))
-> lg 에너지솔루션 보면 처음부터 그려지지 않음
# 계산된 수익률에 대한 기술통계값 구하기
df_norm.describe()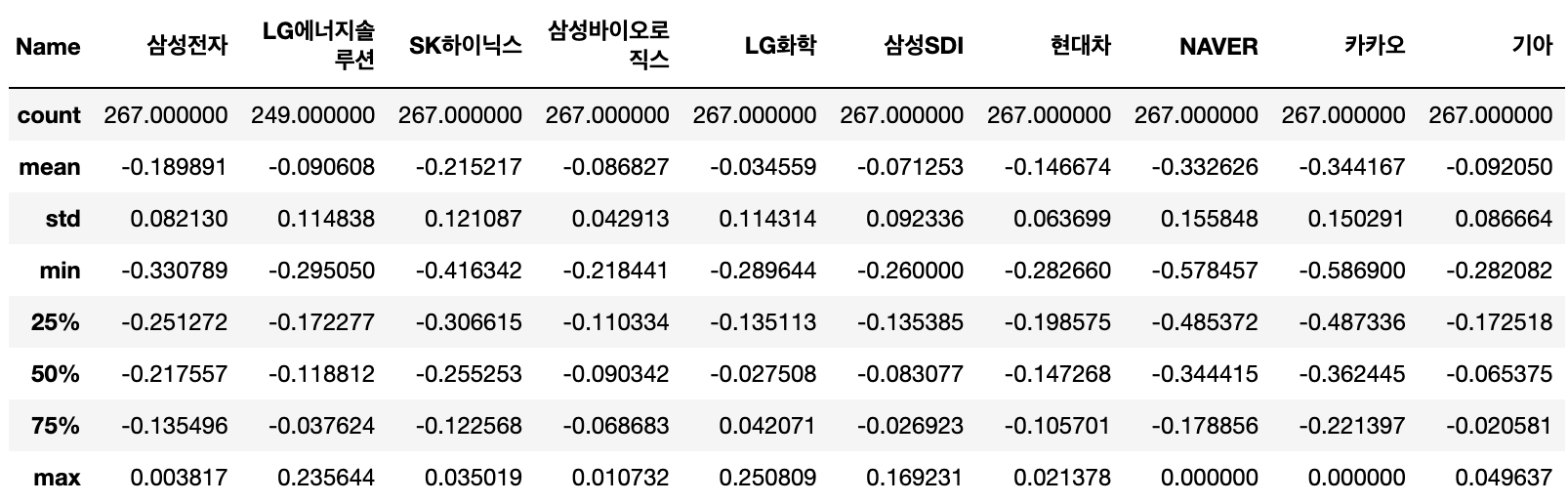
- max 가 0 이면 수익이 생겼던 적이 없다는 의미
- min 손실 이만큼까지 났었다
- mean 평균적으로 어느정도의 수익률인지
- 50% : 한줄로 세워봤을 때 이정도의 수익률이었다 (가운데)
# 수익률에 대한 히스토그램 그리기
df_norm.hist(bins = 50, figsize = (16, 12)) ;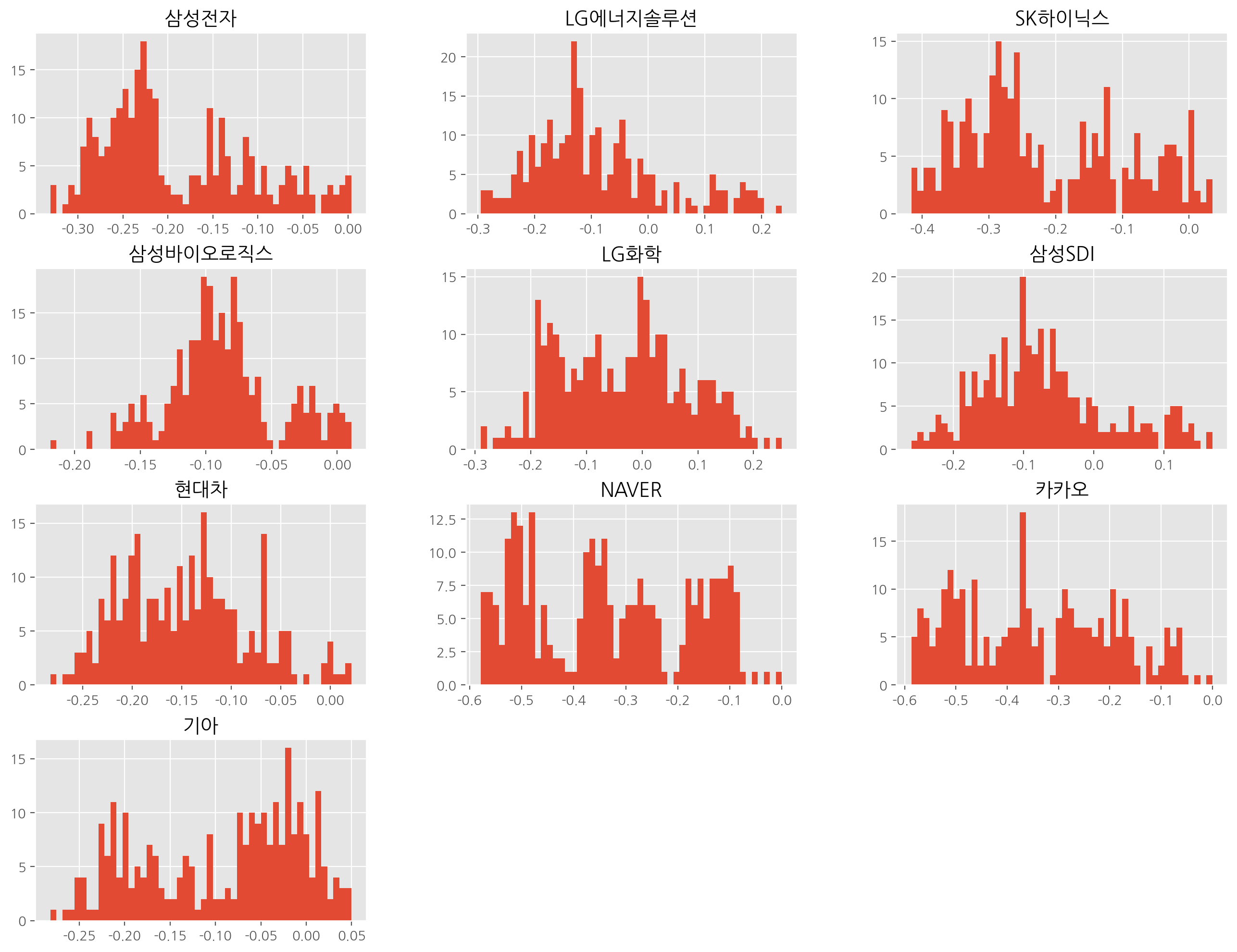
- 0 넘는 곳이 수익이 있던 구간
- 히스토그램을 통해 얻을 수 있는 정보 : 연속된 수치 데이터인지 끊어진 범주형 데이터 인지
-> 범주형 데이터라면 막대가 서로 떨어져 있는데, 주식데이터는 연속된 데이터
- hist 통해서 어느 한 쪽에 몰려있는지 너무 뾰족하지 않은지 알 수 있음 -> 왜도와 첨도
왜도와 첨도
왜도

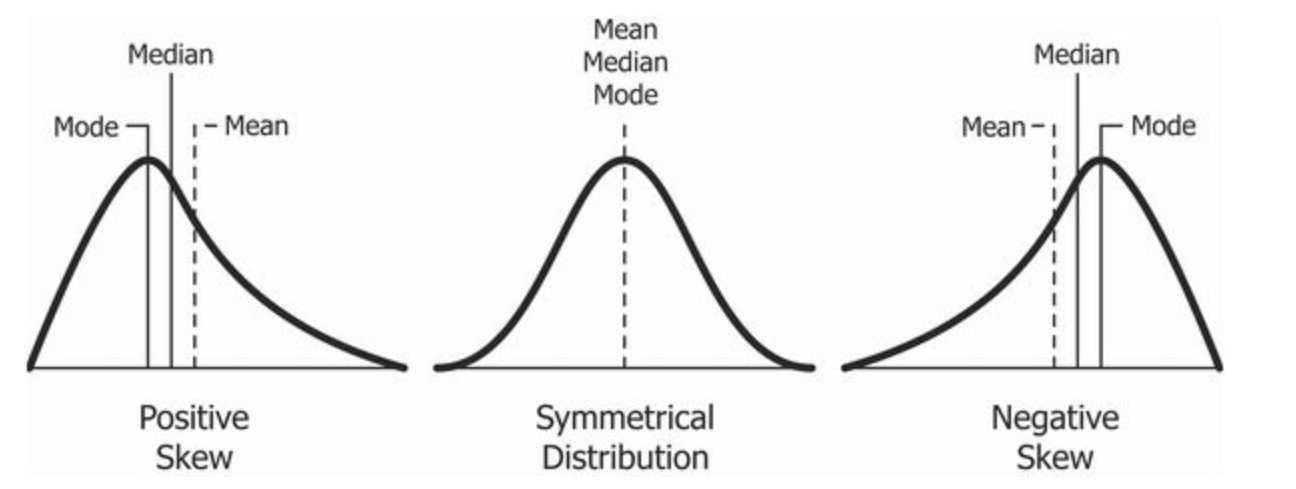
- 비대칭도(非對稱度, skewness) 또는 왜도(歪度)는 실수 값 확률 변수의 확률 분포 비대칭성을 나타내는 지표이다. 왜도의 값은 양수나 음수가 될 수 있으며 정의되지 않을 수도 있다.
- 왜도가 음수일 경우에는 확률밀도함수의 왼쪽 부분에 긴 꼬리를 가지며 중앙값을 포함한 자료가 오른쪽에 더 많이 분포해 있다.
- 왜도가 양수일 때는 확률밀도함수의 오른쪽 부분에 긴 꼬리를 가지며 자료가 왼쪽에 더 많이 분포해 있다는 것을 나타낸다.
- 평균과 중앙값이 같으면 왜도는 0이 된다.
- 출처 : 비대칭도 - 위키백과, 우리 모두의 백과사전
- 정규분포 모양(종모양)이 가장 이상적 but, 현실에서는 종모양 형태 거의 없음 -> 머신러닝, 딥러닝 할 때는 정규분포 형태로 분포의 모양 변경해 주기도 함(아직 잘 모르겠음)
df_norm.skew()
>>
Name
삼성전자 0.622228
LG에너지솔루션 0.807583
SK하이닉스 0.405323
삼성바이오로직스 0.182232
삼성SDI 0.592175
LG화학 0.110345
현대차 0.368547
NAVER 0.125706
기아 -0.357208
카카오 0.193220
dtype: float6첨도

첨도(尖度, 영어: kurtosis 커토시스[*])는 확률분포의 꼬리가 두꺼운 정도를 나타내는 척도
- 극단적인 편차 또는 이상치가 많을 수록 큰 값을 나타낸다.
- 첨도값(K)이 3에 가까우면 산포도가 정규분포에 가깝다.
- 3보다 작을 경우에는(K<3) 산포는 정규분포보다 꼬리가 얇은 분포로 생각할 수 있다
- 첨도값이 3보다 큰 양수이면(K>3) 정규분포보다 꼬리가 두꺼운 분포로 판단할 수 있다.
- 출처 : 첨도 - 위키백과
df.kurt()
>>
Name
삼성전자 -0.600114
LG에너지솔루션 0.195648
SK하이닉스 -1.023456
삼성바이오로직스 0.060285
삼성SDI -0.091909
LG화학 -0.823146
현대차 -0.411500
NAVER -1.255082
기아 -1.188288
카카오 -1.046377
dtype: float64
- 예제를 통해 외우는 것을 추천
- df.index 활용 => 요일변경하기, 서울120 에서 병합을 위해 인덱스값 변경하기
- df.columns 활용 => 교차표구하고 교차표의 요일 번호를 요일명으로 변경하기, 여러 종목의 종가를 수집했을 때 모든 컬럼이 Close 종가로 되어있기 때문에 각 종목명으로 변경해 주는 실습
- concat(axis=0) => 컬럼명이 같은 여러 데이터를 불러와서 병합할 때 , 예, 기간별로 나뉜 데이터
- concat(axis=1) => 인덱스 값이 같은 여러 데이터를 병합 할 때, 예, 여러 주가를 비교할 때
왜도, 첨도 뭔 소리인지 잘 모르겠음
수학 왜 필요한지 이제 알겠음…;;;
'AI SCHOOL > Python' 카테고리의 다른 글
| [Python] 전국 신규 민간 아파트 분양가격 동향 (0) | 2023.02.09 |
|---|---|
| [Python] Plotly / FinanceDataReader (1) | 2023.02.02 |
| [Python] FinanceDataReader - 1 (0) | 2023.01.31 |
| [Python] 서울 코로나 데이터 분석(EDA) - 2 (0) | 2023.01.31 |
| [Python] 서울 코로나 데이터 분석(EDA) - 1 (0) | 2023.01.30 |