- Ordinal Encoding
train['YME'] = train['YM'].astype('category').cat.codes- ExtraTreesRegressor
from sklearn.ensemble import ExtraTreesRegressor
model = ExtraTreesRegressor(random_state=42)- 평가
# R-squared(결정계수)
from sklearn.metrics import r2_score
r2_score(y_train, y_valid_predict)
# MAE(Mean Absolute Error)
# 틀린 값에 대한 절대값만 보고자 한다면
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_train, y_valid_predict)
# MSE(Mean Squared Error)
# 많이 틀릴 수록 패널티를 더 주고자 하면
from sklearn.metrics import mean_squared_error
mean_squared_error(y_train, y_valid_predict)
# RMSE(Root Mean Squared Error)
# 틀린 값에 대한 편차를 보고자 한다면
mean_squared_error(y_train, y_valid_predict)**0.5
# RMSLE(Root Mean Squared Logarithmic Error)
# 적게 틀린 것에 더 패널티를 주고 아주 많이 틀린 것에 좀 더 적게 패널티를 주고자 한다면
from sklearn.metrics import mean_squared_log_error
np.sqrt(mean_squared_log_error(y_train, y_valid_predict))- kaggle 제출
# 답안지 양식을 불러오기
submit = pd.read_csv('data/bike/sampleSubmission.csv')
# 예측한 값을 답안지에 옮겨 적기
submit['count'] = y_predict
# 캐글에 제출하기 위해 csv 파일로 저장
file_name = f'data/bike/sumbit_{rmsle:.5f}.csv'
submit.to_csv(file_name, index = False)
데이터셋 확인 및 전처리
데이터셋: Bike Sharing Demand - Bike Sharing Demand | Kaggle
train = pd.read_csv('data/bike/train.csv')
test = pd.read_csv('data/bike/test.csv')set(train.columns) - set(test.columns)
-> test 데이터에 정답값 없음
- Ordinal-Encoding
- 범주형 변수를 순서 고려한 숫자로 인코딩 하는 방법
- 예를 들어, 학생들의 성적을 A, B, C, D, F로 나타내는 등급 변수가 있다면, 이를 1, 2, 3, 4, 5와 같은 숫자로 변환 -> 이때 숫자는 등급이 높아질수록 증가하도록 부여
- Ordinal Encoding은 One-Hot Encoding과는 달리, 각 범주형 변수마다 새로운 컬럼을 생성하지 않음 -> 데이터 차원 줄일 수 있음
- 범주형 변수의 값이 순서에 따라 일정한 의미를 가질 때(등급, 크기, 순서)에 효과 but, 범주형 변수의 값이 순서와 상관 없는 경우(색상, 국가, 동물)에는 성능 떨어질 수 있음
train["datetime"] = pd.to_datetime(train["datetime"])
train["year"] = train["datetime"].dt.year
train["month"] = train["datetime"].dt.month
train["day"] = train["datetime"].dt.day
train["hour"] = train["datetime"].dt.hour
train["minute"] = train["datetime"].dt.minute
train["second"] = train["datetime"].dt.second
train["dayofweek"] = train["datetime"].dt.dayofweek
train["YM"] = train["datetime"].astype(str).str[:7]
train["YME"] = train["YM"].astype("category").cat.codes
train.iloc[:2, -8:]
-> test도 똑같이 해야
EDA
- histogram 그리기
- 서로 상관관계가 높을 것으로 보이는 열들로 scatter plot 그리기

train[["temp", "atemp"]].corr()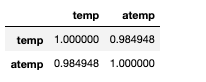
sns.scatterplot(data=train, x="temp", y="atemp")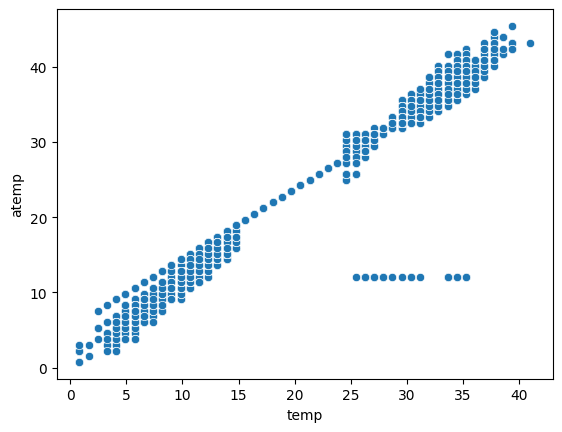
train[(train["temp"] > 25) & (train["atemp"] < 20)]
-> 2012-08-17 0~23 시까지 측정이 잘못되었다고 보여짐
sns.barplot(data=train, x="month", y="count", errorbar=None)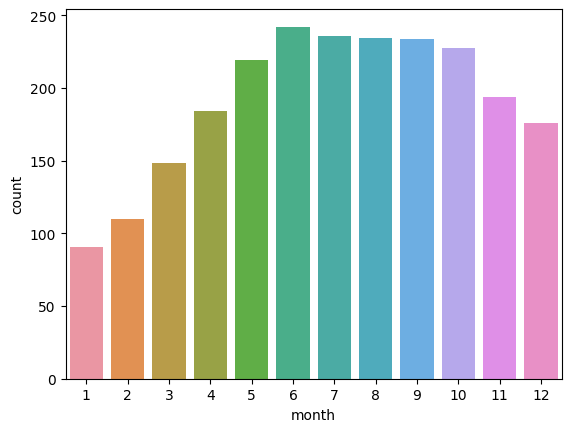
sns.barplot(data=train, x="hour", y="count", errorbar=None)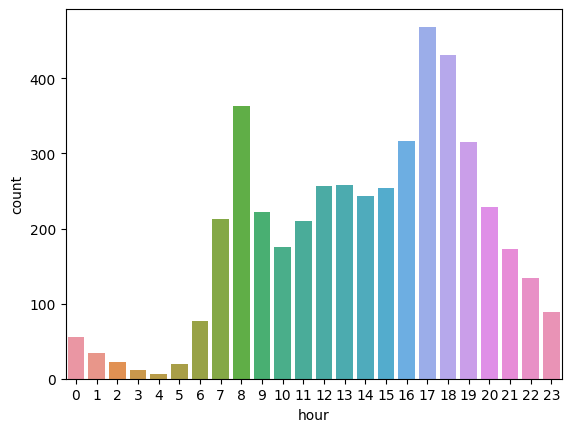
-> y축의 값의 default는 평균 -> count로 시각화하니 전혀 다른 모습을 보임
sns.barplot(data=train, x="day", y="count", errorbar=None)
-> 19일까지 밖에 없음

학습, 예측 데이터셋 나누기
# 정답값
label_name = "count"
# feature_names : 학습, 예측에 사용할 컬럼명(변수)
feature_names = train.columns.tolist()
feature_names.remove(label_name)
feature_names.remove('casual')
feature_names.remove('registered')
feature_names.remove('datetime')
feature_names.remove('minute')
feature_names.remove('second')
feature_names = ['season', 'holiday', 'workingday', 'weather', 'temp',
'atemp', 'humidity', 'windspeed', 'year', 'hour', 'dayofweek']
# 학습에 사용할 데이터셋
X_train = train[feature_names]
# 학습에 사용할 정답값
y_train = train[label_name]
# 예측에 사용할 데이터셋
X_test = test[feature_names]
ExtraTreesRegressor
from sklearn.ensemble import ExtraTreesRegressor
model = ExtraTreesRegressor(random_state=42)
교차검증
from sklearn.model_selection import cross_val_predict
y_valid_predict = cross_val_predict(model, X_train, y_train,
cv=5, n_jobs=-1, verbose=2)
y_valid_predict[:2]
평가
- 회귀 문제는 Accuracy 로 평가가 적합하지 않음
-> 예를 들어 부동산 가격을 예측한다고 했을 때, 억단위 부동산이라면 정확하게 원단위까지 예측하기가 어려움
- R-squared (결정 계수, Coefficient of Determination)
: R-squared는 모델이 실제 데이터를 얼마나 잘 설명하는지를 나타내는 지표
1에 가까울수록 모델이 데이터를 잘 설명한다는 의미입니다. R-squared가 높을수록 모델의 성능이 좋다고 판단 - MAE (Mean Absolute Error)
: MAE는 실제값과 예측값의 차이를 절대값으로 평균한 값
MAE가 작을수록 모델의 성능이 좋다고 판단
틀린 값에 대해 절댓값만 볼 때 - MSE (Mean Squared Error)
: MSE는 실제값과 예측값의 차이를 제곱하여 평균한 값
MSE가 작을수록 모델의 성능이 좋다고 판단
많이 틀릴 수록 패널티를 줄 때 -> 오차에 제곱을 하기 때문 - RMSE (Root Mean Squared Error)
: RMSE는 MSE의 제곱근
따라서 MSE와 달리 단위가 원래 단위로 돌아 옴
RMSE가 작을수록 모델의 성능이 좋다고 판단
틀린 값에 대해 편차를 볼 때 -> 루트를 씌워줘서 MSE보다 이상치에 덜 민감 => 이상치가 크게 중요하지 않을 분야에서 평가할 때 - RMSLE(Root Mean Squared Logarithmic Error)
- 교차 검증한 결과를 평가
# R-squared(결정계수)
from sklearn.metrics import r2_score
r2_score(y_train, y_valid_predict)
# MAE(Mean Absolute Error)
# 틀린 값에 대한 절대값만 보고자 한다면
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_train, y_valid_predict)
# MSE(Mean Squared Error)
# 많이 틀릴 수록 패널티를 더 주고자 하면
from sklearn.metrics import mean_squared_error
mean_squared_error(y_train, y_valid_predict)
# RMSE(Root Mean Squared Error)
# 틀린 값에 대한 편차를 보고자 한다면
mean_squared_error(y_train, y_valid_predict)**0.5
# RMSLE(Root Mean Squared Logarithmic Error)
# 적게 틀린 것에 더 패널티를 주고 아주 많이 틀린 것에 좀 더 적게 패널티를 주고자 한다면
from sklearn.metrics import mean_squared_log_error
np.sqrt(mean_squared_log_error(y_train, y_valid_predict))
학습과 예측
y_predict = model.fit(X_train, y_train).predict(X_test)
제출
# 답안지 양식 불러오기
submit = pd.read_csv("data/bike/sampleSubmission.csv")
# 예측한 값을 답안지에 옮겨 적기
submit["count"] = y_predict
submit.head(3)
# 저장
file_name = f"data/bike/submit_{rmsle:.5f}.csv"
submit.to_csv(file_name, index=False)
- 이상치(outlier)와 오류(error)
- 이상치: 일반적인 값들과 동떨어진 값, 다른 데이터와는 매우 다른 값을 가지는 데이터
- 오류: 데이터 수집 과정에서 발생한 문제로 인한 값
- scatterplot, residplot, regplot
| Scatterplot | - 두 개의 변수 간의 관계를 살펴보는 데에 사용되는 산점도 그래프 - 두 변수 간의 상관 관계를 파악할 수 있으며, 회귀 분석을 수행하기 전에 두 변수 간의 관계를 살펴볼 수 있음 |
| Residplot | - 회귀 분석에서 잔차(residual)를 시각화하는 데에 사용되는 그래프 - 잔차는 예측 값과 실제 값 사이의 차이이며, 잔차가 크면 모델이 정확하지 않은 것을 의미 - residplot을 통해 잔차의 패턴을 파악하여 모델이 적절한지 여부를 판단할 수 있음 |
| Regplot | - 두 변수 간의 선형 회귀 분석 결과를 시각화하는 그래프 - regplot은 scatterplot과 유사하게 두 변수 간의 관계를 살펴보지만, 추가적으로 회귀 분석 결과를 함께 시각화 - 이를 통해 두 변수 간의 선형 관계와 회귀 분석의 적합성을 파악할 수 있음 |
=> catterplot은 두 변수 간의 관계를 파악하기 위해, residplot은 회귀 분석의 잔차를 시각화하기 위해, regplot은 두 변수 간의 선형 회귀 분석 결과를 시각화하기 위해 사용
- 오차(Error)와 잔차(Residual)
| 오차(Error) | 잔차(Residual) | |
| 정의 | 실제값과 예측값의 차이 | 실제값과 모델 예측값의 차이 |
| 계산 방법 | 오차 = 실제값 - 예측값 | 잔차 = 실제값 - 모델 예측값 |
| 특징 | 모델의 정확성 측정 | 모델의 적합성 측정 |
| 사용 | 모델 평가, 예측 성능 평가 | 회귀 분석에서 모델 적합성 평가 |
'AI SCHOOL' 카테고리의 다른 글
| [ML] RandomizedSearchCV (0) | 2023.03.23 |
|---|---|
| [ML] GridSearch / GradientBoostingRegressor (0) | 2023.03.19 |
| [ML] One hot Encoding / ExtraTreesClassifier / cross validation (0) | 2023.03.18 |
| [ML] one-hot encoding / Random Forest (0) | 2023.03.18 |
| [ML] Decision Tree (0) | 2023.03.17 |