모집단과 표본
- 모집단 population
: 연구의 관심이 되는 집단 전체 -> 무한, 실제로 다 보는 것은 불가능(전수조사할 때만 가능 but, 거의 불가능) - 표본 sample
: 특정 연구에서 선택된 모집단의 부분 집합 - 표집 sampling
: 모집단에서 표본을 추출하는 절차. '표본 추출'이라고도 함
-> 대부분의 경우 집단 전체를 전수조사하기는 어려우므로 무작위로 표본 추출하여 모집단에 대해 추론
모수
- 파라미터: 어떤 시스템의 특성을 나타내는 값
- 모수: 모집단의 파라미터 -> 모집단의 특성을 나타내는 값
-> 모수를 구하기 위해서는 전수조사가 필요 (사실상 어려움) / 표본의 크기를 모수라고 하는 경우도 있으나 잘못된 표현!
통계량
- 표본에서 얻어진 수로 계산한 값(= 통계치)
- '모집단의 통계랑'이라는 표현은 없음 -> 통계량은 표본에서 구한 값
- '표본의 모수'라는 말은 없음 -> 모수는 모집단에서 구한 값
- 추론통계 inferential statistics
: 표본 통계량을 일반화하여 모집단에 대해 추론하는 것
-> 계산한 값은 통계랑
모집단에서 구하면 모수, 표본에서 구하면 통계량

표집(= 표본 추출)
- 행동, 모집단에서 표본을 추출하는 절차
- 무작위 표집
: 일정한 확률에 따라 표본을 선택 - 단순 무작위 표집
: 모든 사례를 동일 확률로 추출
- 계통 표집
- 층화 표집
- 집락 표집
계통 표집
- 선거 때 출구조사(투표 후 나와서)
- 단순 무작위 투표 힘듦 -> 투표를 한 사람이 필요한 거니까 -> 투표 후 나온 사람들 중 정해놓은 숫자 n번째 사람이 나오면 물어보는
- 첫 번째 요소는 무작위 선정한 후 목록의 매번 k번째 요소를 표본으로 선정
- 주기성(periodicity)이 있다면 왜곡 가능성
층화 표집
- 모집단을 이루는 각 계층별 무작위 추출
- 모집단이 서로 다른 하위 집단들로 이뤄져 있을 경우에 사용
- 여론조사의 경우 지역별, 연령별, 성별로 나누어 추출
- 여론조사에서 많이 사용 -> 정해진 숫자를 채울 때 까지, 경기도에 사는 30대 여자, 경상도에 사는 20대 남자 등 비율 정해놓고 비율 맞출 때까지 계속 전화
확률표본추출(확률표집) 방법 쉽게 이해하기
오늘은 사회조사분석사나 직업상담사 등 조사 시 표본을 추출해야 할 때 모집단에서 확률적으로 표집 하는 ...
blog.naver.com
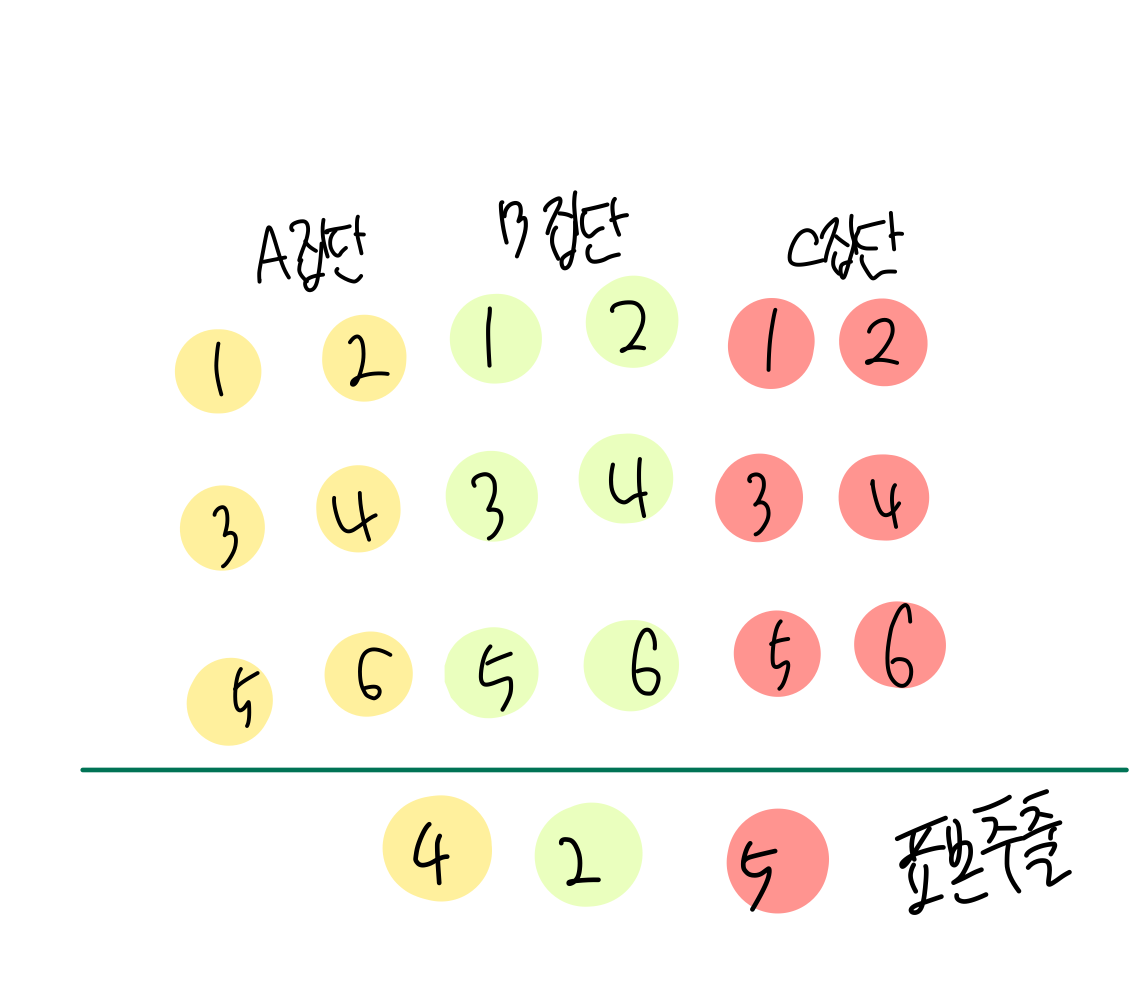
집락 표집
- 모집단을 집락으로 나눈 후 집락 중 일부를 무작위 선택
- ㅇㅇ도시에 고등학교가 여러개, 고등학교마다 수준 비슷해서 무작위로 배정 -> 고등학교 의견 여론조사 하기 위해 이 모든 고등학교 가서 조사하는 것은 어려움 -> 학교 중 일부를 무작위로 고르기 -> 그 학교의 학생들을 조사
표집 분포
- 10개 주사위 돌리면 평균 5.5가 나와야함 그런데 해보니 5.6 나오는 경우 발생 = 모집단이 같아도 통계량은 표본에 따라 달라질 수 있다
- 표집분포: 통계량의 분포
- 표준오차: 표집분포의 표준편차
- 표본의 분포 => 표집분포
1 -> 3 / 2 -> 1 / 3 -> 2 => 4.4
1 -> 2 / 2 -> 3 / 3 -> 1 => 5.6
1-> 4 / 2 -> 2 / 3 -> 2 => 3.8 - 표집분포 실제로 관찰찰하는 값 아님, 이론적 가능성
-> 합계를 구하면 정규분포 형태를 띈다
from scipy.stats import randint
import seaborn as sns
data = randint.rvs(1, 7, size=(5000, 10))
s = data.sum(axis=1)
sns.displot(s, kde=True)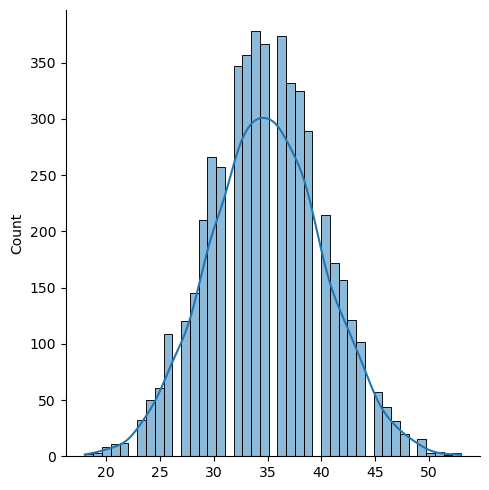
데이터 많이 모아야 하는 이유
- 데이터 많을 수록 표준 오차 작아짐
- 표본의 통계랑이 모수에 더 가깝게 나옴
- 표준오차는 1/√𝑛으로 줄어들기 때문에 데이터를 4배 늘리면 2배 더 정확 -> 평균을 중심으로 그래프가 모임

추정
추정
- 모집단에서 표본을 표집하고 표본에서 통계량을 구하고 거기서 모수를 추측하는 절차를 추정
- 통계량으로 모수를 추측하는 절차
- 점추정 point estimate
: 하나의 수치로 추정 고객 만족도 물어보면 대충 3점 정도 되는 것 같아요 - 구간 추정 interval estimate
: 구간으로 추정 고객만족도 조사해야하는데 얼마야 물어보면 잘 모를 수 있음 2점일 수도 있고 3점일 수도 있는 거 같은데 -> 대충 2~4정도인 것 같아요
신뢰구간
- 대표적인 구간 추정 방법
- 모수가 있을 법한 범위로 추정
- 신뢰구간 = 통계량±오차범위
- 95% 신뢰구간 = 95%의 경우에 모수가 추정된 신뢰구간에 포함 -> 5%의 극단적인 경우는 배제하고
신뢰 수준
- 신뢰구간에 모수가 존재하는 표본의 비율
- 신뢰수준이 높음 -> 많은 표본을 포함(많은 케이스 고려해서 다양한 가능성을 고려) -> 오차범위가 더 넓을 수 밖에 -> 이럴 수도 저럴 수도 있다고 하니 뭘 해야 할 지 알 수 없음 -> 그래서 정보가 적음
- 신뢰 수준이 낮음 -> 90살 까지 산다고 하면 저축하고, 쓰는 돈 어떻게 해야하고 이렇게 계획 세워짐 => 정보 많아짐
=> 신뢰 수준 낮으면 당장 오늘 죽을 경우를 굳이 생각 안 하게 됨 -> 아예 꼭 생각하지 말아야 하는 것은 아니지만 이러한 가능성을 무시하는 것 = 타협 필요 - 신뢰수준이 높음 -> 많은 표본을 포함 -> 더 넓은 오차범위 -> 정보가 적음
- 신뢰수준이 낮음 -> 적은 표본을 포함 -> 더 좁은 오차범위 -> 정보가 많음
- 80세까지 살면 노후대비 -> 나의 평균 수명 예측이 80이지만 모수 속에는 다양한 천재지변 있음(당장 온르 죽으면 어떻게 해야할지 알 수 없음, 수업 들어야 하나? 돈 모아야 하나?) => 알 수 없으니까 정보가 적음
- 신뢰수준 높으면 좋은 건 아님
- 신뢰구간이 좁으면 신뢰수준이 낮으므로 타협이 필요
- 교과서적으로 95%, 99% 등을 추천하나 절대적 기준은 없음
- 감수할 수 있는 수준에서 결정 - 신뢰구간
pip install pingouin
import pingouin as pg
pg.ttest(df.price, 0, confidence=0.95)
평균의 신뢰구간
- 모든 통계량에는 신뢰구간이 존재
- 평균의 경우에는 이론적으로 신뢰구간을 간단히 구할 수 있음
- 다른 통계량은 부트스트래핑 등의 복잡한 계산 필요
부트스트래핑
- 평균과 달리 중간값, 최빈값 등의 통계량은 표집분포의 형태를 간단히 알기 어려움
- 표본이 충분히 크면 부트스트래핑이라는 시뮬레이션 기법을 사용해서 신뢰구간 추정
-> 부트스트래핑은 단일 랜덤 표본에서 복원으로 여러 표본을 가져와서 표본 추출 분포를 추정하는 방법
import scipy
scipy.stats.bootstrap([df.price], np.mean)
scipy.stats.bootstrap([df.price], np.median, confidence_level=0.99)
신뢰구간에 영향을 주는 요소
- 신뢰구간이 좁을 수록 예측된 모수의 범위가 좁으므로 유용
- 신뢰수준 낮추기 -> 큰 의미 없음
- 표본의 변산성 낮추기
- 실험과 측정을 정확히 해서 변산성을 낮춤 -> 일정하게 나오니까
- 데이터에 내재한 변산성은 없앨 수 없음 -> 그런데 배달 같은건 내가 어떻게 할 수 없음, 실험을 정확히 한다해도 없앨 수 없는 것들이 존재함 -> 날씨 예측하는데 기압을 정확하게 잴 수는 있음, 풍속 등 -> 그런데 기압 자체가 들쑥날쑥 하는 건 우리가 어떻게 할 수 있는 일이 아님 => 한계가 있다 - 표본의 크기를 키우기: 가장 쉬운 방법이긴 하지만 시간과 비용이 증가
- 아반떼 오차범위 50만원 내외 , k3 53만원 내외인 이유는 k3가 적게 있기 때문에
여론조사의 '표본오차' 항목
- 국내 여론조사 결과에서 '표본오차'항목이 존재
- 표본 오차: 모집단과 표본의 차이
- 오차 범위: 표본오차의 범위 - 중심극한정리에 따라 신뢰수준 95%에서 오차범위는 다음과 같이 계산

- 1.96: 신뢰수준 95%에 해당하는 값(신뢰수준 99%일 경우 2.58로 계산)
- 0.5: 여론조사의 오차범위는 찬성 50%를 기준으로 계산
- N: 설문 응답자 수

천 후보 10.9%, 황 후보 7.8% 약 3% 차이 나는데 오차범위 +-2.8%포인트이기 때문에 크게 의미부여를 할 필요가 없지 않을까
질문
신제품 개발을 위해 여론조사를 하려고 하는데 일단 대략적인 여론만 알면되기 때문에 오차범위가 플마 십퍼센트포인트 정도만 되면 괜찮을 것 같다 그러면 여론조사를 몇명에게 하면 될까
1.96*0.5/np.sqrt(95)
>> 0.10054587850434511인원수 = (98 / 오차범위) ** 2
통계적 가설 검정
통계적 가설 검정
- 반증주의 철학에 기반하고 있어 일반적인 과학적 가설 검정과 다름
- 많은 비판이 있으나 오랫동안 쓰여왔기 때문에 여전히 널리 쓰임
- 일반적, 과학적 가설검정: "실증주의" -> 내가 하고싶은 주장이 있으면 그걸 지지하는 근거를 가져와서 입증하는 루트
- 통계적 가설검정: "반증주의" -> 미운놈 -> 반대되는 근거 -> 박살…!
-> 너 니 말에 책임질 수 있어 ? 이런… -> 남의 말에 트집 잡고 틀린거 보여주기 위한 ? 이런 느낌
통계적 가설 검정의 절차
- 귀무가설을 수립한다 -> 없애버릴 가설을 준비
- 귀무가설: 기각하고자 하는 가설
- 대립가설: 주장하고자 하는 가설 -> 있는데 무의미 - 유의수준을 결정한다
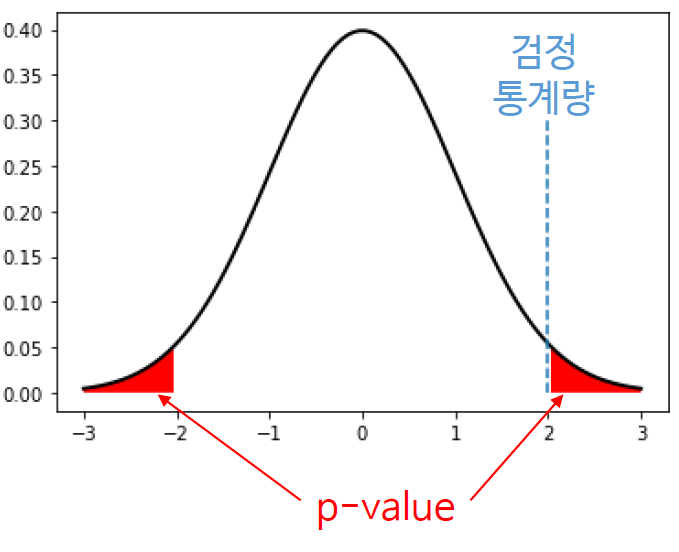
- 유의수준: 100% - 신뢰수준(신뢰수준이 95%면, 5%가 유의수준) - p-값을 계산한다
- p-값: 귀무가설이 참일 때 검정통계량 이상이 나올 확률 (귀무가설을 지지하는 정도, 참이면 숫자가 커짐) - p값과 유의수준을 비교한다
- p>유의수준
- 결론을 유보한다 -> 넘는다고 결론이 나는 것은 아님
- 결론을 내릴 필요가 있을 경우 데이터를 더 모은다
- 단, 반복해서 가설검정을 할 경우 유의수준을 조정 - p<유의수준
- 귀무가설을 기각
- 흔히 '통계적으로 유의하다'라고 표현(현실적으로 유의미한 것은 아님)
pvalue 계산해서 5% 밑이면 깨버린다 5% 못넘엇지!

Python에서 평균의 가설 검정
- 귀무가설이 모평균 = 900일 경우
pg.ttest(df.price, 900, confidence=0.95)
p-val = 0.02
유의수준 = 0.05
p<유의수준 -> 기각!
- 귀무가설 바꿔도 신뢰구간은 바뀌지 않음(전혀 상관 없는 데이터로 계산하는 것이기 때문에 -> 신뢰구간은 가설과 상관 없음 )
- 신뢰구간이 [814.1, 893.22] 근데 모평균 900은 신뢰구간 안에 들어가지도 않음 -> 0.5 넘으면 모평균이 신뢰구간 안에 들어감

통계적 가설 검정 순서도

데이터 더 모아서 100명 중에서 효과 안 봣는데 1000명 해서 한명 효과 보면 이게 무슨 의미?
가설 검정의 결과
| 가설검정 실제 |
귀무가설 기각 |
귀무가설 기각 못함 |
| 귀무가설 참 |
1종 오류 | |
| 귀무가설 거짓 |
2종 오류 |
- 두 가지 오류 있을 수 있음
- 귀무가설이 참인데 기각하는 경우를 1종 오류라고 함 (ex: 배 나온 남성에게 임신이라고 하는 것)
: 귀무가설이 참일 경우 1종 오류는 유의수준만큼 발생(5%) - 귀무가설이 거짓인데 기각하지 못하는 경우를 2종 오류라고 함 (ex: 임신한 여성에게 임신이 아니라고 하는 것)
- 유의수준 낮추면 1종 오류 감소, 2종 오류 증가 -> 유의 수준 너무 낮추면 좋은 약인데 우리가 놓칠 수 있음
- 1종 오류와 2종 오류는 반비례 관계
[질문]
p값 < 유의수준 일때, 귀무가설이 깨진다고 설명해주셨는데, 모평균의 값이 밖에 있으니, 귀무가설은 깨지는 것은 이해 하지만 이게 왜 통계적으로 유의하고, 이 경우가 왜 통계적으로 성과가 있다는 건지?
-> 피셔의 비뚫어진 마음: 귀무가설을 부숴버리겠어! -> 내가 부수고 싶은 걸 부쉈으니 의미있는 결과
대립가설을 채택한다고 해도, 대립가설도 마찬가지로 통계적 가설 검증을 통해 마찬가지로 깨질 수도 있는 거 아닌가?
-> 대립가설에는 사실 별로 관심이 없음
-> 대립가설은 가설검정을 할 수 없음
귀무가설 overtime =12 -> 구체적인 형태이기 때문에 맞다 아니다 검증 가능
대립가설: overtime =/ 12 -> 흐리멍텅한 형태
밥먹으러가자
뭐먹을래 피자? -> 구체적 주장
피자는 별로 -> 주장을 기각만 한 것 => 대립가설
A/B 테스팅
A/B 테스팅
- 과학 분야에서 무작위 대조군 시험 Randomized Controlled Trials(무작위 대조군 실험)
- 주로 웹 서비스 등의 분야에서 A/B테스팅이라는 명칭을 사용
- 고객들에게 서로 다른 웹 페이지나 광고를 보여주고 목표 지표(예: 전환율)을 측정
이중맹검(환자, 의료진 A, B 모르게) / 삼중맹검(분석가까지 모르게)
근거 기반 의학에서 근거의 수준
- Level I: 무작위 대조군 실험에서 얻어진 근거 -> a/b테스팅
- Level II-1: 대조군 실험에서 얻어진 근거(무작위 할당이 아님)
- Level II-2: 동일 집단 연구 등
- Level II-3: 대조군이 없는 극적인 결과 등
- Level III: 임상 경험에 근거한 전문가의 의견 등 -> 근거로 부족
A/B 테스팅에서 중요한 점
- 작은 실험 자주, 많이 해야 함
- 실험 많이 할 수 있는 기술적, 문화적 환경의 형성
독립표본 t - 검정
집단 비교 통계 처리 순서도

- 비교해야 하는 종속변수가 연속형(ex: 매출)일때와 범주형 (ex: 구매/비구매)일 때 다르고,
- 비교하는 집단의 수가 2개 일 때와 2개 이상일 때가 다르다
두 집단의 평균 차이
- 이전에 했던 것은 하나의 평균에 대한 신뢰구간, 평균에 대한 가설 검정
- 이번에는 두 개의

- 두 집단의 모집단이 모두 정규분포를 따르거나 또는 각 집단의 크기가 충분히 큰 경우(𝑛 > 30) t-분포를 이용해서 𝑋1−𝑋2의 신뢰구간을 계산
- 가설검정의 경우 독립표본 t-검정 을 수행
독립표본 t 검정 순서도

- 귀무가설 : 두 평균이 같다는 말은 곧 평균차이 = 0이라는 말
- 귀무가설을 기각한다는 것은 두 집단의 평균이 다르다는 것


[정리]
- 귀무가설: 두 집단(anante와 k3)의 평균이 같다

- 표본에서 k3가 Avante 보다 평균 80만원이 더 비싸다 모집단에서도?

귀무가설은 모집단에서 평균차이 = 0, k3평균 = Avante 평균이라는 것
p-value를 보니 0.05보다 작음 -> 귀무가설 기각
신뢰구간을 보면 더 확실하게 알 수 있음
둘의 신뢰구간은 8만원~152만원(신뢰구간) => 이 말은 모집단에서는 K3가 Avante보다 못해도 8만원, 많게는 152만원 비쌀 것이라는 의미
k3는 Avante보다 비싸다
신뢰구간이 -~+일 때는 이미 같다는 것이 신뢰구간 안에 포함되어 귀무가설 기각할 수 없다
'AI SCHOOL' 카테고리의 다른 글
| [ML] Clustering (0) | 2023.03.12 |
|---|---|
| [통계분석] 상관분석 / 회귀분석 (0) | 2023.02.16 |
| [통계분석] 확률분포 / 정규분포 / 기술통계(분위수, 편차) (0) | 2023.02.13 |
| [WIL] 4주차 (0) | 2023.01.19 |
| [WIL] 3주차 (0) | 2023.01.12 |